02/05/2016
Se revisaron los enlaces l y II.
Además se dieron indicaciones para la redacción de preguntas y se estableció el contenido que debe tener cada trabajo para la presentación final.
- Marco teórico (Información sobre el tema a tratarse como conceptos, qué aspectos conlleva, cómo se divide, etc.)
- Diseño del cuestionario.
- Establecer muestra
- Prueba piloto (aplicada a 10 personas.)
- Aplicación de la encuesta.
- Análisis de los datos.
- Presentación del informe
Clase N° 6
04/05/2016
ESTADÍSTICA DESCRIPTIVA
1. RECOPILACIÓN DE DATOS
1.1. Fuentes
1.2 Criterios para disuadir la encuesta
1.2.1 Tema
1.2.2 Problema (Marco teórico de referencia)
1.2.3 Objetivos: General y específico
1.2.4 Justificación
1.2.5 Referencias (Escritas con normas APA)
1.3 Tipos de datos
1.3.1 Cualitativos o categóricos: Estado civil, género,cédula de identidad, raza, entre otros
1.3.2 Cuantitativos o numéricos
1.3.2.1 Discretos: 1,2,3,4.... (Conteos)
1.3.2.2 Continuos: Dentro de un intervalo
2. SIMBOLOGÍA: Representación de términos para poder simplificarlos, deben estar especificados en el documento.
N: tamaño de la población
n: tamaño de la muestra
X: característica de interés
x: valor de la característico
3. DESCRIPCIÓN DEL CONJUNTO DE DATOS
Los datos podemos representarlos en forma de tablas, gráficos y números, que caracterizan al conjunto de datos.
4.-TABLAS DE FRECUENCIAS:
Facilita la interpretación de datos.
4. 1 Identificar la unidad de medida de los datos
4.2 Obtener el rango de los datos
Rango: R= Xmáx - Xmín
4.3 Selección del número de clase o intervalos:

4.4 Longitud de clases:
L= R/k
4.5 Realizar el conteo de datos para obtener la frecuencia en cada clase
n # de datos
k # de clases
fi frecuencia de las clase
fr: frecuencia relativa de la clase

Fi frecuencia acumulada de la clase

Fr frecuencia acumulada relativa

m marca de la clase i (valor central de la clase)
4.6 Organizar la información en la tabla de frecuencias
Clase N° 7
09/05/2016
PARA DATOS CUALITATIVOS
Para datos cualitativos se utilizan únicamente gráficos de barras y diagrama circular.
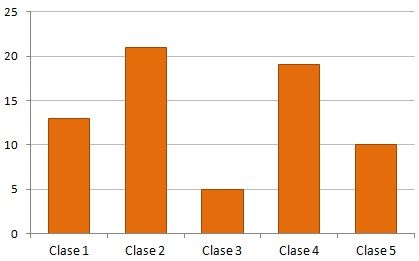

Polígono de Frecuencias
Forma de representación del perfil de la distribución de los datos, se obtiene uniendo mediante segmentos los puntos medios de cada clase (marcas de clase). Para crear el polígono se agrega un punto a cada lado de frecuencia cero.

Ojiva
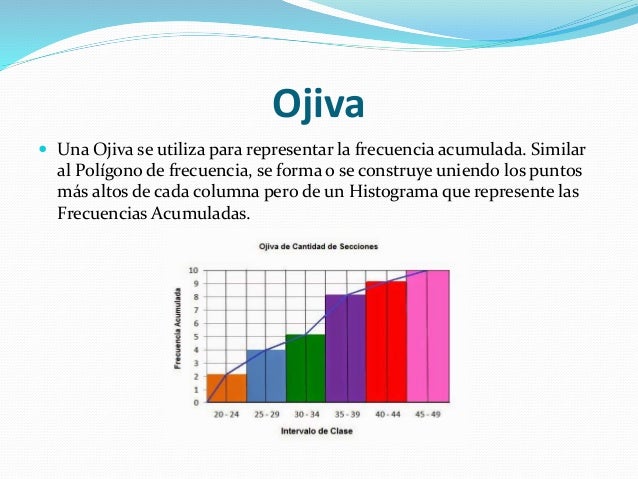
Clase N° 8
Diagrama de Puntos
Un diagrama de puntos es una gráfica utilizada para ilustrar un número reducido de datos, la cual permite identificar con facilidad dos características:
1. La localización de los datos.
2. La dispersión o variabilidad de los datos.
Este diagrama muestra cada uno de los elementos de un conjunto de datos numéricos por encima de una recta numérica (eje horizontal), facilita la ubicación de los espacios vacíos y los agrupamientos en un conjunto de datos, así como la manera en que estos datos se distribuyen a los largo del eje horizontal.

Diagrama de tallo y hojas
Es un método de análisis de datos exploratorio que permite clasificar los datos y observar las frecuencias mayores y menores del conjunto.

Diagrama de Pareto
Identifica las causas principales que producen cierto resultado.
La ley de Pareto dice que de cualquier conjunto de eventos que pueden asociarse a un suceso, solamente unos pocos contribuyen en forma significativa, mientras que los otros son secundarios. Generalmente existen solo 2 o 3 causas significativas.
Procedimiento:
1. Categorice los datos por tipo de problema.
2. Determine la frecuencia y ordene en forma decreciente.
3. Represente la frecuencia relativa con barras.
4. Superponga la ojiva de la frecuencia acumulada.
5. Analice las causas más importantes del problema de estudio.

Clase N° 9
PARA DATOS CUALITATIVOS
Para datos cualitativos se utilizan únicamente gráficos de barras y diagrama circular.

Diagrama de barras

Ejemplo diagrama circular para la distribución de la población mundial por continentes
Polígono de Frecuencias
Forma de representación del perfil de la distribución de los datos, se obtiene uniendo mediante segmentos los puntos medios de cada clase (marcas de clase). Para crear el polígono se agrega un punto a cada lado de frecuencia cero.

Ojiva

Clase N° 8
11/05/2016
Diagrama de Puntos
Un diagrama de puntos es una gráfica utilizada para ilustrar un número reducido de datos, la cual permite identificar con facilidad dos características:
1. La localización de los datos.
2. La dispersión o variabilidad de los datos.
Este diagrama muestra cada uno de los elementos de un conjunto de datos numéricos por encima de una recta numérica (eje horizontal), facilita la ubicación de los espacios vacíos y los agrupamientos en un conjunto de datos, así como la manera en que estos datos se distribuyen a los largo del eje horizontal.

Diagrama de tallo y hojas
Es un método de análisis de datos exploratorio que permite clasificar los datos y observar las frecuencias mayores y menores del conjunto.

Diagrama de Pareto
Identifica las causas principales que producen cierto resultado.
La ley de Pareto dice que de cualquier conjunto de eventos que pueden asociarse a un suceso, solamente unos pocos contribuyen en forma significativa, mientras que los otros son secundarios. Generalmente existen solo 2 o 3 causas significativas.
Procedimiento:
1. Categorice los datos por tipo de problema.
2. Determine la frecuencia y ordene en forma decreciente.
3. Represente la frecuencia relativa con barras.
4. Superponga la ojiva de la frecuencia acumulada.
5. Analice las causas más importantes del problema de estudio.

Clase N° 9
16/05/2016
Se realizó la actividad en clase 1 referente a la aplicación de los distintos tipos de gráficos estadísticos, según el tipo de variables.
Clase N° 10
CÁLCULO DE MEDIDAS
Únicamente para datos cuantitativos, son las siguientes:

1. De Localización:
i) Datos individuales:
 ii) Datos individuales con frecuencias:
ii) Datos individuales con frecuencias:
 iii) Datos agrupados en intervalos:
iii) Datos agrupados en intervalos:
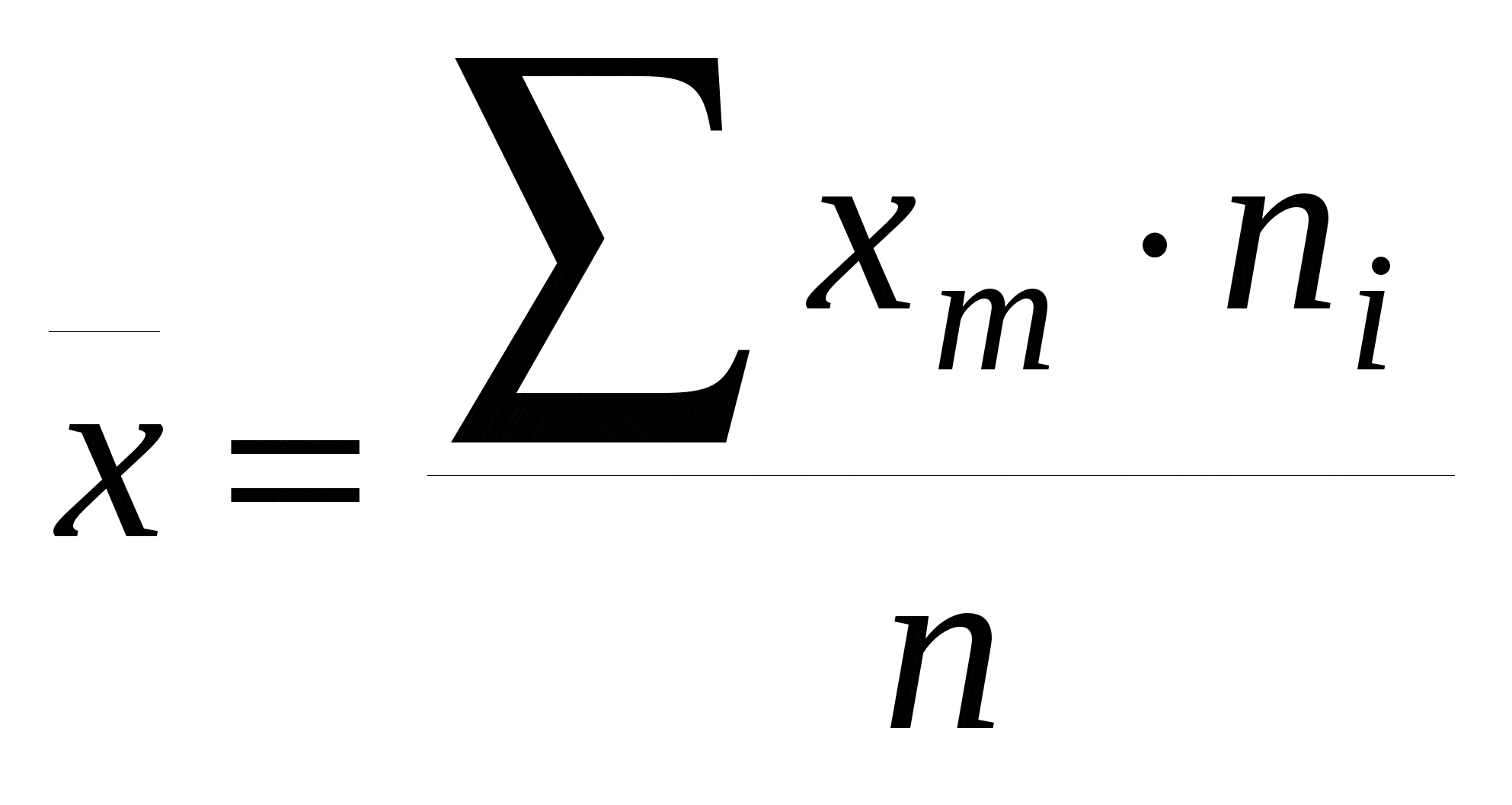
i) Datos individuales:
 ii) Datos agrupados en intervalos:
ii) Datos agrupados en intervalos:
2. De Dispersión:
i) Datos individuales:

ii) Datos individuales con frecuencias:

iii) Datos agrupados en intervalos:

i) Datos individuales:
 ii) Datos individuales con frecuencias:
ii) Datos individuales con frecuencias:

iii) Datos agrupados en intervalos:

 Si CV<= 1 entonces, los datos son homogéneos.
Si CV<= 1 entonces, los datos son homogéneos.
Si CV> 1,5 entonces, los datos son heterogéneos.
Clase N° 11
Se realizó la actividad en clase 1 referente a la aplicación de los distintos tipos de gráficos estadísticos, según el tipo de variables.
Clase N° 10
18/05/2016
CÁLCULO DE MEDIDAS
Únicamente para datos cuantitativos, son las siguientes:

1. De Localización:
- Media: La media aritmética de n valores, es igual a la suma de todos ellos dividida entre n.
i) Datos individuales:


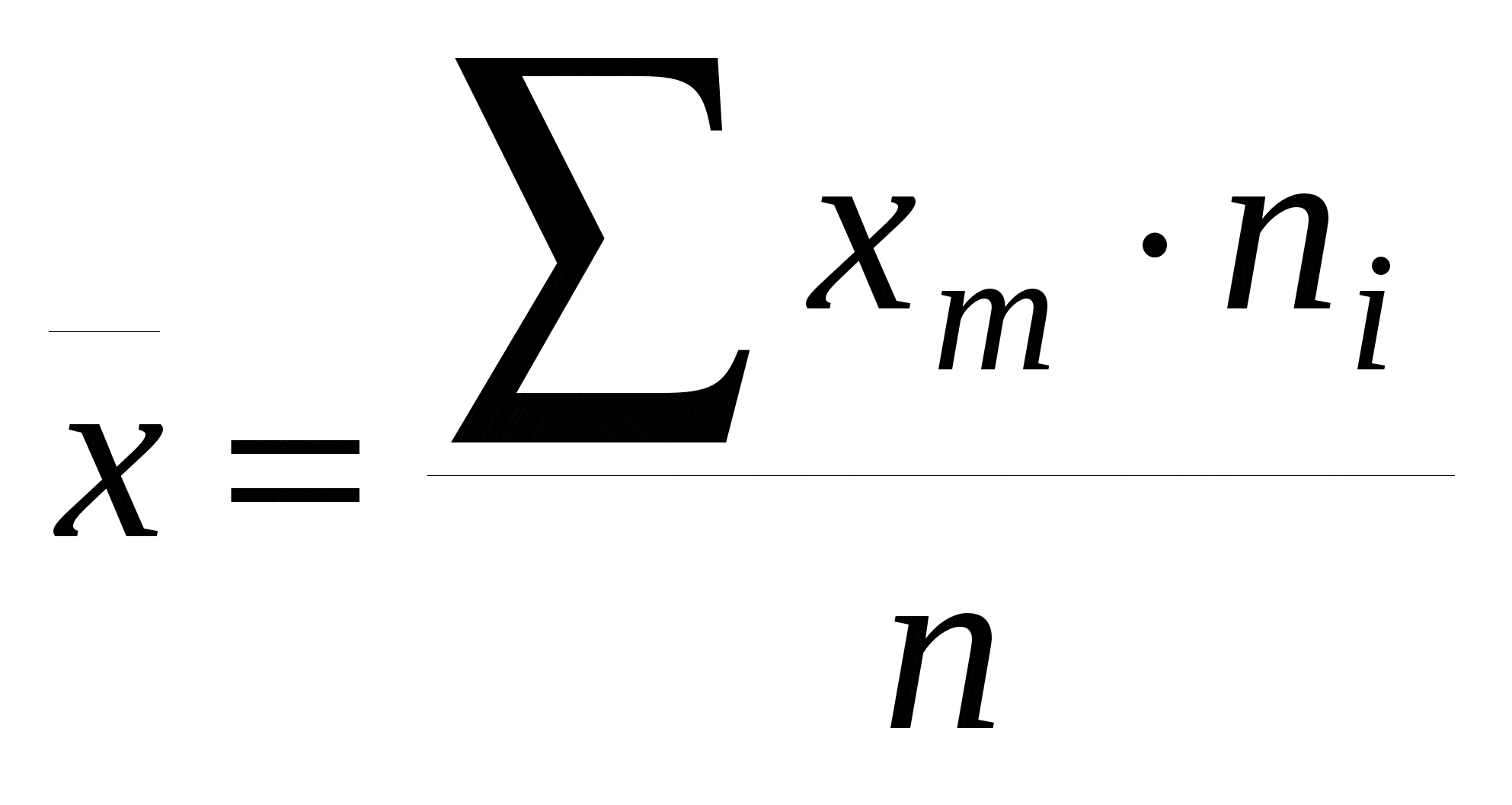
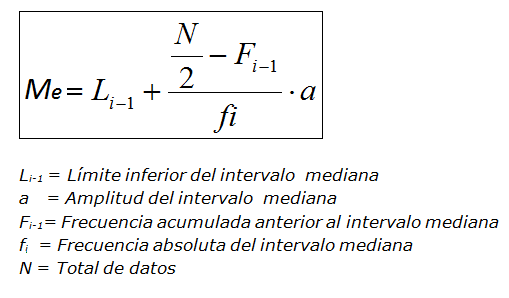
- Mediana: es el punto central de una serie de datos ordenados de forma ascendente.
i) Datos individuales:


- Moda: La moda de un conjunto de datos numéricos es el valor que más se repite, es decir, el que tiene el mayor número de frecuencias absolutas. La moda puede ser no única e inclusive no existir.
2. De Dispersión:
- Rango: El rango de una distribución es la diferencia entre el valor máximo y el valor mínimo de la variable estadística. Para su cálculo, basta con ordenar los valores de menor a mayor.
R= Xmax - Xmin
- Varianza: La varianza mide la mayor o menor dispersión de los valores de la variable respecto a la media aritmética. Cuanto mayor sea la varianza mayor dispersión existirá y por tanto, menor representatividad tendrá la media aritmética. La varianza se expresa en las mismas unidades que la variable analizada,pero elevadas al cuadrado.
i) Datos individuales:

ii) Datos individuales con frecuencias:

iii) Datos agrupados en intervalos:

- Desviación estándar: o desviación típica es la raíz cuadrada de la varianza, es decir, la raíz cuadrada de la media de los cuadrados de las puntuaciones de desviación.
i) Datos individuales:


iii) Datos agrupados en intervalos:

- Coeficiente de variación (CV): Este coeficiente, representa el porcentaje que la desviación estándar contiene a la media aritmética y por lo tanto cuanto mayor es CV mayor es la dispersión y menor la representatividad de la media.

Si CV> 1,5 entonces, los datos son heterogéneos.
Clase N° 11
23/05/2016
- Percentiles: son cada una de las 99 divisiones que dividen a la distribución de datos en 100 partes iguales.
Para determinar los percentiles se debe:
1. Hallar:

3. Si los datos son agrupados:
 Lk-1: límite inferior de la clase de interés.
Lk-1: límite inferior de la clase de interés.
Nk-1: frecuencia absoluta acumulada del intervalo inmediatamente anterior al intervalo de interés.
fk: frecuencia absoluta del intervalo de interés.
A: amplitud del intervalo de interés.
- Cuartiles: son cada una de las 3 divisiones que dividen a la distribución de datos en 4 partes iguales. Los cuartiles corresponden a los percentiles número 25, 50 y 75.
- Deciles: son cada una de las 9 divisiones que dividen a la distribución de datos en 10 partes iguales. Los deciles corresponden a los percentiles número 10, 20, 30, 40, 50, 60, 70, 80 y 90.
OBSERVACIÓN: La mediana de un conjunto de datos, equivale al percentil número 50 y al cuartil número 2.
El diagrama de caja es un gráfico utilizado para representar una variable cuantitativa (variable numérica). El gráfico es una herramienta que permite visualizar, a través de los cuartiles, cómo es la distribución, su grado de asimetría, los valores extremos, la posición de la mediana.
Se compone de:

Clase N° 12
- MEDIDAS DE POSICIÓN
- Percentiles: son cada una de las 99 divisiones que dividen a la distribución de datos en 100 partes iguales.
Para determinar los percentiles se debe:
1. Hallar:
n: tamaño de la muestra.
k: orden del percentil.
t: parte entera del resultado.
r: fracción del resultado.
2. Si los datos son individuales:
3. Si los datos son agrupados:

Nk-1: frecuencia absoluta acumulada del intervalo inmediatamente anterior al intervalo de interés.
fk: frecuencia absoluta del intervalo de interés.
A: amplitud del intervalo de interés.
- Cuartiles: son cada una de las 3 divisiones que dividen a la distribución de datos en 4 partes iguales. Los cuartiles corresponden a los percentiles número 25, 50 y 75.
- Deciles: son cada una de las 9 divisiones que dividen a la distribución de datos en 10 partes iguales. Los deciles corresponden a los percentiles número 10, 20, 30, 40, 50, 60, 70, 80 y 90.
OBSERVACIÓN: La mediana de un conjunto de datos, equivale al percentil número 50 y al cuartil número 2.
- DIAGRAMA DE CAJAS
El diagrama de caja es un gráfico utilizado para representar una variable cuantitativa (variable numérica). El gráfico es una herramienta que permite visualizar, a través de los cuartiles, cómo es la distribución, su grado de asimetría, los valores extremos, la posición de la mediana.
Se compone de:
- Un rectángulo (caja) delimitado por el primer y tercer cuartil (Q1 y Q3). Dentro de la caja una línea indica dónde se encuentra la mediana (segundo cuartil Q2)
- Dos brazos, uno que empieza en el primer cuartil y acaba en el mínimo, y otro que empieza en el tercer cuartil y acaba en el máximo.
- Los datos atípicos (o valores extremos) que son los valores distintos que no cumplen ciertos requisitos de heterogeneidad de los datos.

Clase N° 12
25/05/2016
4. MEDIDAS DE FORMA

 - Coeficiente de apuntamiento (Ap)
- Coeficiente de apuntamiento (Ap)
 Si Ap > 0, la distribución es Leptocurtica.
Si Ap > 0, la distribución es Leptocurtica.
Si Ap = 0, la distribución es Mesocurtica.
Si Ap < 0, la distribución es Platicurtica.

Clase N° 12
Existen casos que los datos de las muestras miden dos características, siendo entonces importante determinar si existe alguna relación entre ellas.
1. Diagrama de Dispersión de datos:






4. MEDIDAS DE FORMA
- Coeficiente de asimetría (As): Pretende establecer la simetría de la distribución de los datos.

Si As > 0, la distribución es asimétrica a la derecha con respecto a la media.
Si As = 0, la distribución presenta simetría con respecto a la media.
Si As < 0, la distribución es asimétrica a la izquierda con respecto a la media.


Si Ap = 0, la distribución es Mesocurtica.
Si Ap < 0, la distribución es Platicurtica.

Clase N° 12
25/05/2016
MUESTRAS BIVARIADASExisten casos que los datos de las muestras miden dos características, siendo entonces importante determinar si existe alguna relación entre ellas.
1. Diagrama de Dispersión de datos:

La distribución conjunta de dos variables puede expresarse gráficamente mediante un diagrama de dispersión: en un plano se representa cada elemento observado haciendo que sus coordenadas sobre los ejes cartesianos sean los valores que toman las dos variables para esa observación.
2. Correlación:
Es frecuente que se estudie sobre una misma población los valores de dos variables estadísticas distintas, con el fin de ver si existe alguna relación entre ellas, es decir, si los cambios en una de ellas influyen en los valores de la otra. Si ocurre esto se dice que las variables están correlacionadas o bien que hay correlación entre ellas.

3. Covarianza muestral:
La covarianza es una medida de la asociación lineal entre dos variables que resume la información existente en un gráfico de dispersión.

4. Coeficiente de correlación (r):
Permite cuantificar el grado de correlación lineal existente entre dos variables.

i) Si r tiene valor cercano a 1, correlación fuerte positiva.
ii) Si r tiene valor cercano a -1, correlación fuerte negativa.
iii) Si r tiene valor cercano a 0, correlación débil o no hay correlación.
5. Matriz de varianzas y covarianzas:

6. Matriz de correlación:

No hay comentarios:
Publicar un comentario